Um sistema está isolado quando contido por paredes adiabáticas, ou seja, quando não pode trocar energia na forma de calor com a vizinhança.
É um fato experimental que um sistema isolado sempre tende a um estado de equilíbrio térmico, isto é, um estado para o qual as variáveis macroscópicas que o caracterizam não mudam com o tempo.
Quando dois sistemas estão separados por uma parede diatérmica dizemos que estão em contato térmico.
Colocando em contato térmico dois sistemas que, isoladamente, estavam em equilíbrio térmico, observam-se mudanças em suas variáveis macroscópicas até que alcancem novos valores que permanecem constantes com o tempo. Dizemos, então, que os dois sistemas estão em equilíbrio térmico um com o outro.
O conceito de temperatura está associado ao seguinte fato experimental, conhecido como lei zero da termodinâmica: dois sistemas em equilíbrio térmico com um terceiro estão em equilíbrio térmico ente si.
Assim, dois sistemas em equilíbrio térmico entre si estão à mesma temperatura.
Para saber se dois sistemas têm a mesma temperatura não é necessário colocá-los em contato térmico entre si, bastando verificar se ambos estão em equilíbrio térmico com um terceiro corpo, chamado termômetro.
Na prática, um termômetro pode ser construído como segue.
Escolhe-se uma substância termométrica. Por exemplo, o mercúrio.
Escolhe-se, desta substância, uma propriedade que dependa da percepção fisiológica de temperatura. Por exemplo, o volume.
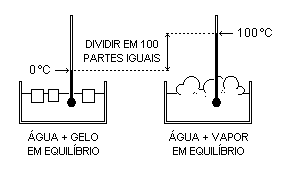
Define-se a escala de temperatura. A escala Celsius, por exemplo, é definida por dois pontos fixos e uma lei linear.

As leis físicas são expressas por equações matemáticas mais simples se a temperatura é dada na escala Kelvin:

T[K] = 273 + t[oC]

O estado de um gás ideal fica definido pelas variáveis macroscópicas: pressão (P), volume (V) e temperatura Kelvin (T).
As variáveis pressão e temperatura representam valores médios de grandezas microscópicas.
A pressão está relacionada com o valor médio da quantidade de movimento transferida das partículas às paredes do recipiente nas colisões.
A temperatura está relacionada com a energia cinética média das partículas.
A relação matemática entre estas variáveis é chamada equação de estado.
Gás ideal é aquele para o qual vale a equação de estado (de Clapeyron):

PV = nRT

para quaisquer valores de P e T.
Aqui, n é o número de mols da substância em questão e R, a constante universal dos gases.

Lei de Charles

Para uma transformação isovolumétrica (a volume constante):

P / T = constante

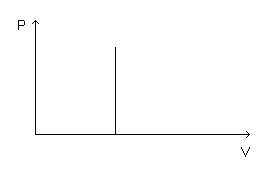
Assim, para uma dada massa de gás mantido o volume constante, a pressão é diretamente proporcional à temperatura absoluta.

Lei de Gay-Lussac

Para uma transformação isobárica (a pressão constante):

V / T = constante

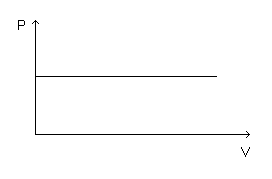
Assim, para uma dada massa de gás mantida a pressão constante, o volume é diretamente proporcional à temperatura absoluta.

Lei de Boyle-Mariotte

Para uma transformação isotérmica (a temperatura constante):

PV = constante

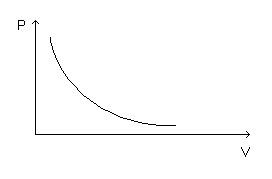
Assim, para uma dada massa de gás mantida a temperatura constante, a pressão é inversamente proporcional ao volume ocupado.

Os valores atribuídos à temperatura de um sistema qualquer dependem do termômetro usado, mesmo que todos concordem nos pontos fixos que definem a escala usada.
Existe, portanto, a necessidade de escolher um termômetro padrão, pelo menos para uso científico. O termômetro escolhido como padrão é o termômetro de gás a volume constante.

Um gás enche um bulbo e um capilar ligado a um manômetro de tubo aberto com mercúrio. O bulbo é colocado em contato térmico com o sistema cuja temperatura se quer determinar.
Um tubo flexível permite levantar ou abaixar um reservatório com mercúrio, fazendo com que o mercúrio no ramo esquerdo do manômetro coincida sempre com o zero da escala.
Assim, o volume do gás pode ser mantido constante, apesar do aumento ou diminuição da sua temperatura.
Neste termômetro, a propriedade termométrica é a pressão do gás.
Medindo-se h, o desnível do mercúrio no manômetro, e conhecendo-se o valor da pressão atmosférica, PA, o módulo da aceleração da gravidade, g, e a densidade do mercúrio, r, a pressão do gás no bulbo é determinada por:

P = PA + rgh

A temperatura do gás e, portanto, do sistema em questão, é definida em função de um ponto fixo, o ponto triplo da água, por:

T(P) = 273,16 [ P / PT ] K

onde PT é a pressão do gás quando em contato com a água no ponto triplo.
O ponto triplo representa o estado em que coexistem, em equilíbrio, as fases líquida, sólida e gasosa da água. Para esse estado, P = 4,58 mmHg e T = 0,01 oC.
Na prática, mede-se PT e P para quantidades cada vez menores de gás (ou seja, para PT tendendo a zero) e a temperatura é tomada como o resultado desse processo de limite.
A escala de temperatura assim definida depende apenas das propriedades gerais dos gases e não das propriedades de um gás particular.
Como os gases reais se comportam como ideais no limite de baixas pressões, esta escala é chamada de escala termométrica de gás ideal.
Então, o termômetro usada como padrão é o termômetro de gás a volume constante com a escala termométrica de gás ideal.
A escala escolhida desta maneira independe das propriedades de qualquer gás em particular, mas depende das propriedades dos gases ideais.
A escala termométrica absoluta Kelvin independe das propriedades de qualquer substância. A escala Kelvin e a escala de gás ideal são idênticas no intervalo de temperatura em que o termômetro de gás pode ser usado.

A força externa que atua sobre um elemento de superfície da fronteira do sistema de área DA é:

DFE = - PE DA

e se esse elemento de superfície sofre um deslocamento Ds, o trabalho desta força externa sobre ele é:

D2 WE = DFEDs = - PE DA Ds

Quando todos os elementos de superfície são incluídos, o trabalho das forças externas (da vizinhança) sobre o sistema é dado pela soma de D2 WE sobre toda a superfície de área A, resultando:

DWE = - PE DV

Esta expressão dá o trabalho da vizinhança sobre o sistema quando o volume do sistema sofre uma variação muito pequena DV.

O trabalho da vizinhança sobre o sistema é positivo quando DV < 0, ou seja, quando o sistema se contrai.
O trabalho da vizinhança sobre o sistema é negativo quando DV > 0, ou seja, quando o sistema se expande.
Quando a variação de volume do sistema é finita, pode-se pensar que ela se dá por uma série de etapas, cada qual associada a uma variação de volume muito pequena. Então, o trabalho total da vizinhança sobre o sistema é a soma dos trabalhos associados a cada etapa:

WE = - S PE DV

Por outro lado, pela terceira lei de Newton, as forças externas que atuam sobre o sistema são iguais em módulo e direção, mas de sentido contrário, às forças do sistema sobre a vizinhança.
Assim, podemos escrever, para o trabalho do sistema sobre a vizinhança, quando o volume do sistema sofre uma variação muito pequena DV:

DW = - DWE = PE DV

Agora, caso o processo de variação de volume do sistema seja reversível, tem sentido falar na pressão P do sistema, com P = PE. Então:

DW = P DV

Esta expressão dá o trabalho do sistema sobre a vizinhança quando o volume do sistema sofre uma variação muito pequena DV.

O trabalho do sistema sobre a vizinhança é positivo quando DV > 0, ou seja, quando o sistema se expande.
O trabalho do sistema sobre a vizinhança é negativo quando DV < 0, ou seja, quando o sistema se contrai.
Para uma transformação reversível finita no volume do sistema:

W = S P DV

A relação entre a pressão e o volume (dada pela equação de estado) de um sistema que se transforma reversivelmente pode ser representada por uma curva no plano P-V.

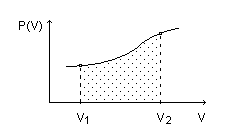
A área entre a curva e o eixo OV, de V1 até V2, representa o trabalho do sistema contra a vizinhança numa expansão de V1 até V2.
A partir dessa interpretação geométrica para o trabalho podemos ver claramente que o mesmo depende do processo que liga os estados inicial e final, já que então a área correspondente deve ser diferente.
Para um processo de expansão isobárico reversível:

W = P ( V2 - V1 )

e caso o sistema seja um gás ideal:

W = nR ( T2 - T1 )

Para um processo de expansão isotérmico reversível de um gás ideal:

W = nRT ln ( V2 / V1 )